For storing permanent information about a world in Postgres, WorldQL offers the abstraction of Records.
Records have two goals:
- Offer fast lookups that leverage database indexes
- Partition the data into multiple tables to save time building indexes and allow for easier scaling
Our solution was to build an octree-inspired data structure with customizable degree and depth. This results in an n-tree, which supports dividing cubic areas into a customizable number of slices, not just 8.
As records represent permanent alterations in the world, clients will almost always want to fetch the full set of objects in a roughly defined area. Therefore, extensions like PostGIS are a bit overkill. We only need to be able to roughly grab all records in a given set of areas.
The structure of the database n-tree is decided by four configuration variables set as environment variables:
- WQL_LEAF_SQUARE_SIZE
- WQL_TREE_DEGREE (must be a cubic number)
- WQL_NUM_LEVELS
- WQL_ROOTS_PER_TABLE (must be a cubic number)
For Minecraft, we want to group changes by chunks at the smallest level. So we'd set the variables to:
- WQL_LEAF_SQUARE_SIZE = 16, each partition contains objects in a 16x16 area, which correspond to sections of a chunk.
- WQL_TREE_DEGREE = 512, further index on 8x8 chunk sets
- WQL_NUM_LEVELS = 2, only two levels including the leaf and root nodes
- WQL_ROOTS_PER_TABLE = 8, a 2x2 cube which means each 256-wide area receives its own table
This configuration would result in a scheme where:
- Each object is stored in 16 unit wide cube "buckets" which are the leaf nodes in the tree
- 512 leafs are stored in each tree root representing a 128x128x128 unit wide space.
- 8 roots per table, meaning each table represents a 256x256 cube area
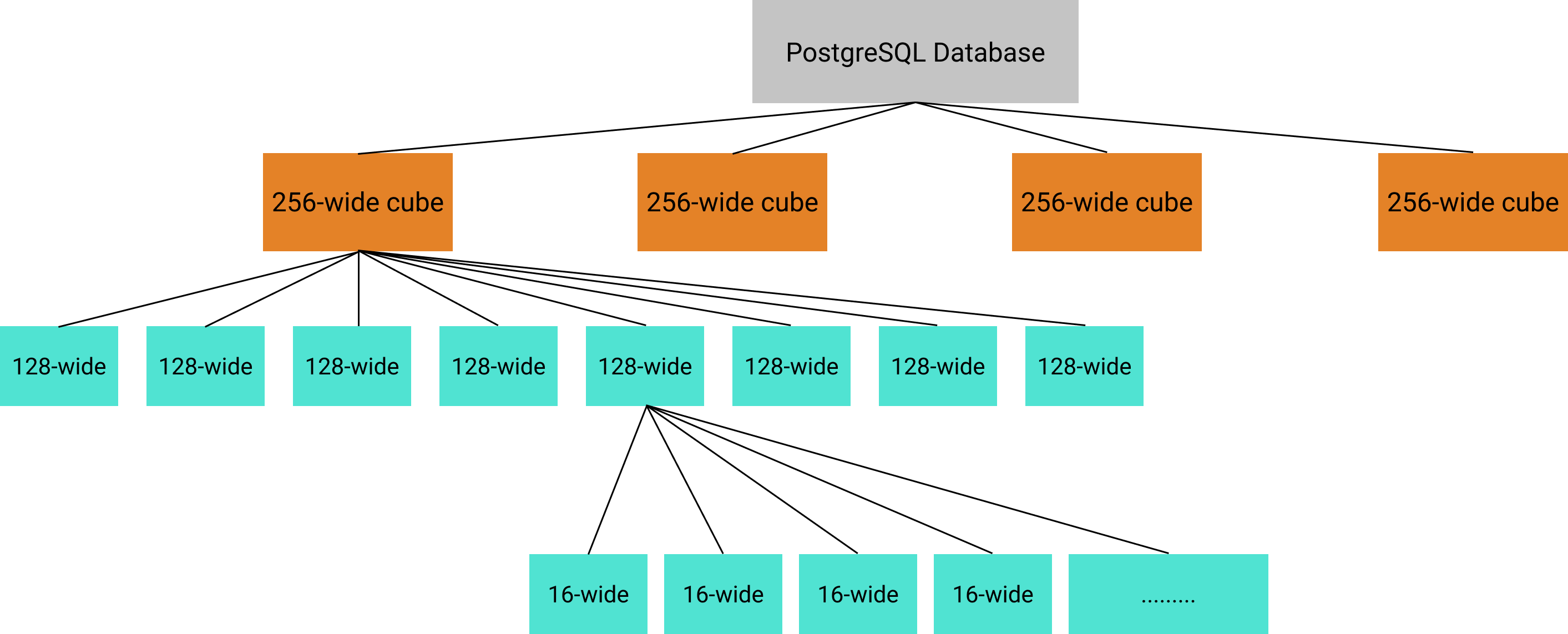
Orange nodes represent tables, while teal ones represent column values.
In our example system, there are an arbitrary number of tables depending on how much of the world contains objects. For each table, there are eight (WQL_ROOTS_PER_TABLE) children of each table node. Each of those nodes has 512 children representing 16x16 areas which are not fully shown.
Every table has a compound index on its child key columns (teal nodes), which each refer to an n-tree child with a single integer. For our example, there are only two node child key columns, so a compound index offers good performance.
Thanks for reading, feel free to leave questions or comments in our Discord.